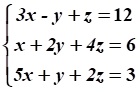МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. О. СУХОГО
Факультет автоматизированных и информационных систем
Кафедра «Информационные технологии»
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 3
по дисциплине «Численные методы математической физики»
на тему: «Составление и отладка программ по методам решения систем линейных алгебраических уравнений (СЛАУ)»
Выполнил: студент гр. ИТП-21
Bob X А.В.
Принял: преподаватель
Стародубцев Е.Г.
Гомель 2018
Цель работы: научиться разрабатывать алгоритмы численных методов и программное обеспечение для решения СЛАУ.
ЗАДАНИЕ
Разработать алгоритмы и написать программы, реализующие следующие методы решения СЛАУ:
1. метод Гаусса;
2. метод LU-разложения (в двух модификациях: 1) с единицами на главной диагонали матрицы U; 2) с единицами на главной диагонали матрицы L);
3. метод прогонки;
4. метод простой итерации;
5. метод Гаусса-Зейделя.
Варианты заданий
| 3 |
Задание 1. Метод Гаусса
Первый этап решения системы уравнений по методу Гаусса, называемый прямым ходом метода Гаусса, заключается в приведении расширенной матрицы к треугольному виду. Это означает, что все элементы матрицы ниже главной диагонали должны быть равны нулю
Для формирования первого столбца матрицы необходимо из каждой строки (начиная со второй) вычесть первую, умноженную на некоторое число Мi.
Коэффициент М для i-й строки выбирается из условия
, и равен
![]()
![]()
![]()
![]()
Очевидно, что если повторить описанный выше алгоритм для следующих столбцов матрицы, причем начинать преобразовывать второй столбец с третьего элемента, третий столбец — с четвертого и т.д.
В результате выполнения прямого хода метода Гаусса матрица преобразуется в матрицу, а система уравнений будет иметь следующий вид:

Решение системы называют обратным ходом метода Гаусса. Формула для вычисления i-го значения x будет иметь вид:
![]()
Код программы:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 | #include <iostream> #include <math.h> #include <windows.h> using namespace std; void sysout(double **a, double *y, int n) { for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { cout << a[i][j] << "*x" << j; if (j < n - 1) cout << " + "; } cout << " = " << y[i] << endl; } return; } double * gauss(double **a, double *y, int n) { double *x, max; int k, index; const double eps = 0.00001; x = new double[n]; k = 0; while (k < n) { max = abs(a[k][k]); index = k; for (int i = k + 1; i < n; i++) { if (abs(a[i][k]) > max) { max = abs(a[i][k]); index = i; } } if (max < eps) { cout << "Решение получить невозможно из-за нулевого столбца "; cout << index << " матрицы A" << endl; return 0; } for (int j = 0; j < n; j++) { double temp = a[k][j]; a[k][j] = a[index][j]; a[index][j] = temp; } double temp = y[k]; y[k] = y[index]; y[index] = temp; for (int i = k; i < n; i++) { double temp = a[i][k]; if (abs(temp) < eps) continue; for (int j = 0; j < n; j++) a[i][j] = a[i][j] / temp; y[i] = y[i] / temp; if (i == k) continue; for (int j = 0; j < n; j++) a[i][j] = a[i][j] - a[k][j]; y[i] = y[i] - y[k]; } k++; } for (k = n - 1; k >= 0; k--) { x[k] = y[k]; for (int i = 0; i < k; i++) y[i] = y[i] - a[i][k] * x[k]; } return x; } int main() { double **a, *y, *x; int n; system("chcp 1251"); system("cls"); cout << "Введите кол-во уравнений: "; cin >> n; a = new double*[n]; y = new double[n]; for (int i = 0; i < n; i++) { a[i] = new double[n]; for (int j = 0; j < n; j++) { cout << "a[" << i << "][" << j << "]= "; cin >> a[i][j]; } } for (int i = 0; i < n; i++) { cout << "y[" << i << "]= "; cin >> y[i]; } sysout(a, y, n); x = gauss(a, y, n); for (int i = 0; i < n; i++) cout << "x[" << i << "]=" << x[i] << endl; cin.get(); cin.get(); return 0; } |
Результат выполнения:

Задание 2. Метод LU-разложения
, где A={} – квадратная матрица порядка n.

Следовательно, вектор x можно вычислить из системы
причем она легко решается, так как матрицы L и U – треугольные.
Метод LU разложения с единицами на главной диагонали матрицы L. Представим матрицу в виде произведения треугольных матриц

Таким образом, решение системы с квадратной матрицей коэффициентов сводится к решению двух систем с треугольными матрицами коэффициентов:


Код программы:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 | #include "pch.h" #include <iostream> #include <vector> #include <math.h> #include <windows.h> using namespace std; void LU(vector <vector <double> > A, vector <vector <double> > &L, vector <vector <double> > &U, int n) { U = A; for (int i = 0; i < n; i++) for (int j = i; j < n; j++) L[j][i] = U[j][i] / U[i][i]; for (int k = 1; k < n; k++) { for (int i = k - 1; i < n; i++) for (int j = i; j < n; j++) L[j][i] = U[j][i] / U[i][i]; for (int i = k; i < n; i++) for (int j = k - 1; j < n; j++) U[i][j] = U[i][j] - L[i][k - 1] * U[k - 1][j]; } } void proisv(vector <vector <double> > A, vector <vector <double> > B, vector <vector <double> > &R, int n) { for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) for (int k = 0; k < n; k++) R[i][j] += A[i][k] * B[k][j]; } void show(vector <vector <double> > A, int n) { for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { cout << "\t" << A[i][j] << "\t"; } cout << endl; } } int main() { int n = 3,koef; vector <vector <double> > A(4), L(n), U(n), R(n); for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { cin >> koef; A[i].push_back(koef); L[i].push_back(0); U[i].push_back(0); R[i].push_back(0); } } LU(A, L, U, n); cout << "Fisrt matrix" << endl; show(A, n); cout << "U matrix" << endl; show(U, n); cout << "L matrix" << endl; show(L, n); proisv(L, U, R, n); cout << "L*U matrix" << endl; show(R, n); return 0; } |


Задание 3. Метод прогонки

где i=1, 2, n, = 0, = 0. Такие уравнения называют трехточечными разностными уравнениями второго порядка. Для решения систем существует специальный метод, называемый методом прогонки. Заключается он в следующем. Предположим, что существуют такие наборы чисел , для которых


Необходимо выяснить сходимости этого метода.
Необходимо преобразовать матрицу, чтобы данное условие выполнялось:
- 3 -1 1 12
- 1 2 4 6
- 5 1 2 3
Выполним преобразование С = С-A:
- 3 -1 1 12
- 1 2 4 6
- 2 2 1 -9
Далее выполним еще раз С= С-А
- 3 -1 1 12
- 1 2 4 6
- -1 3 0 -21
Поменяем местами B и C
- 3 -1 1 12
- -1 3 0 -21
- 1 2 4 6
Код программы:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 | #include "pch.h" #include <iostream> #include "conio.h" #include "math.h" #include "iostream" using namespace std; int i, n, k, n1; double z; double A[50][50]; double B[50]; double eps[50]; double X[50]; double et[50]; int main() { cout << "Vvedite razmernost matrici: "; cin >> n1; cout << "Vvedite " << n1 << " strok po " << n1 << " 4isel:" << endl; for (i = 0; i < n1; i++) for (k = 0; k < n1; k++) cin >> A[i][k]; cout << "Matrix A:" << endl; for (i = 0; i < n1; i++) { for (k = 0; k < n1; k++) cout << A[i][k] << "\t "; cout << endl; } cout << "Vvedite " << n1 << " 4isel:" << endl; for (i = 0; i < n1; i++) cin >> B[i]; cout << "Matrix B:" << endl; for (i = 0; i < n1; i++) cout << B[i] << endl; n = n1 - 1; eps[0] = -A[0][1] / A[0][0]; et[0] = B[0] / A[0][0]; for (i = 1; i < n; i++) { z = A[i][i] + A[i][i - 1] * eps[i - 1]; eps[i] = -A[i][i + 1] / z; et[i] = (B[i] - A[i][i - 1] * et[i - 1]) / z; } X[n] = (B[n] - A[n][n - 1] * et[n - 1]) / (A[n][n] + A[n][n - 1] * eps[n - 1]); for (i = n - 1; i >= 0; i--) X[i] = eps[i] * X[i + 1] + et[i]; cout << "Matrix X:" << endl; for (i = 0; i < n1; i++) cout << X[i] << endl; _getch(); return 0; } |

Задание 4. Метод итерации

или в развернутом виде:
![]()

Алгоритм метода простой итерации заключается в следующем:
- Проверка условий (2.36), если они не выполняются, то работа алгоритма завершена, иначе переходим к п.2.
- Формирование матрицы α и массива β по формулам (2.31).
- Формирование начального приближения по (2.33).
- Расчет нового приближения по (2.34).
- Если условие (2.35) выполняется и максимальная ошибка вычислений меньше заданного числа ε, то решение найдено, иначе переходим к п.4.
Необходимо выяснить являются ли преобладающими диагональные элементы. Это очень важный шаг, проверяется условие сходимости этого метода. Нужно чтобы оно выполнялось. Для нашей системы данное условие не выполняется.
Необходимо преобразовать матрицу, чтобы данное условие выполнялось:
- 3 -1 1 12
- 1 2 4 6
- 5 1 2 3
Выполним преобразование С = С-A:
- 3 -1 1 12
- 1 2 4 6
- 2 2 1 -9
Далее выполним еще раз С= С-А
- 3 -1 1 12
- 1 2 4 6
- -1 3 0 -21
Поменяем местами B и C
- 3 -1 1 12
- -1 3 0 -21
- 1 2 4 6
Код программы:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 | #include "pch.h" #include <iostream> #include <locale> #include <cmath> #include <iomanip> #include <iostream> using namespace std; double f1(double x1, double x2, double x3); double f2(double x1, double x2, double x3); double f3(double x1, double x2, double x3); double g1(double x1, double x2, double x3); double g2(double x1, double x2, double x3); double g3(double x1, double x2, double x3); double shag = 0.0005; //Шаг приращения int main() { setlocale(LC_ALL, "Russian"); cout << "\tВведите начальное приближение, свободные члены\n"; double x1; cout << "x1 = "; cin >> x1; double x2; cout << "x2 = "; cin >> x2; double x3; cout << "x3 = "; cin >> x3; double er; cout << "Введите погрешность = "; cin >> er; for ( double it = 0; er < fabs(f1(x1, x2, x3)) || er < fabs(f2(x1, x2, x3)) || er < fabs(f3(x1, x2, x3)); it = it + 1 ) { cout << "Итерация # " << setprecision(0) << it << endl; cout << "x1 " << setprecision(0) << (x1 = g1(x1, x2, x3)) << endl; cout << "x2 " << setprecision(0) << (x2 = g2(x1, x2, x3)) << endl; cout << "x3 " << setprecision(0) << (x3 = g3(x1, x2, x3)) << endl; } cout << "f1(x1, x2, x3) = " << f1(x1, x2, x3) << endl; cout << "f2(x1, x2, x3) = " << f2(x1, x2, x3) << endl; cout << "f3(x1, x2, x3) = " << f3(x1, x2, x3) << endl; system("pause"); return 0; } double f1(double x1, double x2, double x3) { return 3 * x1 - x2 + x3 - 12; } double f2(double x1, double x2, double x3) { return -1*x1 + 3*x2 + 0 * x3 + 21; } double f3(double x1, double x2, double x3) { return x1 + 2 * x2 +4*x3 - 6; } double g1(double x1, double x2, double x3) { return x1 - shag *f1(x1, x2, x3); } double g2(double x1, double x2, double x3) { return x2 - shag *f2(x1, x2, x3); } double g3(double x1, double x2, double x3) { return x3 - shag *f3(x1, x2, x3); } |


Задание 5. Метод Зейделя

Выполним следующие преобразования:
![]()
Пусть:
![]()
Тогда система:
![]()
эквивалентна системе и обладает следующими свойствами:

Необходимо выяснить сходимости этого метода.
Необходимо преобразовать матрицу, чтобы данное условие выполнялось:
- 3 -1 1 12
- 1 2 4 6
- 5 1 2 3
Выполним преобразование С = С-A:
- 3 -1 1 12
- 1 2 4 6
- 2 2 1 -9
Далее выполним еще раз С= С-А
- 3 -1 1 12
- 1 2 4 6
- -1 3 0 -21
Поменяем местами B и C
- 3 -1 1 12
- -1 3 0 -21
- 1 2 4 6
Код программы:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 | #include "pch.h" #include <iostream> #include <iomanip> #include <cmath> #include <windows.h> using namespace std; class Matr { private: int size; double **mas; double *mas1; public: Matr() { size = 0; mas = NULL; mas1 = NULL; } Matr(int l) { size = l; mas = new double*[l]; for (int i = 0; i < l; i++) mas[i] = new double[l]; mas1 = new double[l]; } void Add() { for (int i = 0; i < size; i++) for (int j = 0; j < size; j++) cin >> mas[i][j]; for (int i = 0; i < size; i++) { cin >> mas1[i]; } } void Print() { for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { cout << setw(4) << mas[i][j] << " "; } cout << " " << mas1[i] << endl; } } void Preob() { double temp = 0; for (int k = 0; k < size; k++) { for (int i = 0; i < size; i++) { temp = mas[i][i] * (-1); mas1[i] /= temp; for (int j = 0; j <= size; j++) { mas[i][j] /= temp; } } } for (int i = 0; i < size; i++) { mas1[i] *= -1; for (int j = 0; j < size; j++) mas[i][i] = 0; } } double Pogr(double **mas, double epsilon) { double eps = 0; double sum = 0, max = 0; double norm1 = 0, norm2 = 0; for (int i = 0; i < size; i++) { for (int j = 0; j < i; j++) { sum += fabs(mas[i][j]); if (sum > norm1) norm1 = sum; } sum = 0; for (int j = i + 1; j < size; j++) { sum += fabs(mas[i][j]); if (sum > norm2) norm2 = sum; } sum = 0; } if (norm1 >= 1 || norm2 >= 1) { cerr << "Норма матрицы больше или равна 1,т.е. не имеет решения" << endl; Sleep(4000); exit(1); } eps = ((1 - norm1) / norm2)*epsilon; return eps; } void Itera(double epsilon) { double *x = new double[size]; double *p = new double[size]; double *a = new double[size]; double *E = new double[size]; double per = Pogr(mas, epsilon), max = 0; for (int i = 0; i < size; i++) { x[i] = mas1[i]; p[i] = 0; } double var = 0; for (int i = 0; i < size; i++) { var = 0; for (int k = 0; k < size; k++) var = mas[i][k] * mas1[k]; x[i] = var; } for (int i = 0; i < size; i++) p[i] = x[i] + mas1[i]; int counter = 0; do { counter++; cout << "Итерация № " << counter << endl << endl; for (int i = 0; i < size; i++) { var = 0; for (int j = 0; j < i; j++) var += (mas[i][j] * p[j]); for (int j = i + 1; j < size; j++) var += (mas[i][j] * x[j]); a[i] = var; x[i] = mas1[i] + a[i]; } max = 0; for (int i = 0; i < size; i++) { E[i] = fabs(x[i] - p[i]); if (max < E[i]) max = E[i]; p[i] = x[i]; cout << "x" << i + 1 << "=" << x[i] << " " << endl; } cout << endl; cout << "max =" << max << endl << endl; } while (max > per); cout << endl << "Результат: \n\n"; for (int i = 0; i < size; i++) cout << "x" << i + 1 << "=" << x[i] << " " << endl; delete[] x; delete[] p; delete[] E; delete[] a; } ~Matr() { for (int i = 0; i < size; i++) delete mas[i]; delete mas; } }; int main() { setlocale(LC_ALL, "rus"); int n; double epsi; cout << "Введите количество уравнений: "; cin >> n; cout << "Введите желаемую точность: "; cin >> epsi; Matr a(n); cout << "Введите матрицу коэффициентов, потом столбец свободных членов:" << endl; a.Add(); cout << endl << "Расширенная матрица:" << endl; a.Print(); a.Preob(); cout << endl << "Преображенная матрица" << endl; a.Print(); cout << endl; a.Itera(epsi); cout << endl; system("pause"); return 0; } |
Результат выполнения программы:


Вывод: научились разрабатывать алгоритмы численных методов и программное обеспечение для решения СЛАУ.